Rifle, Handgun & Shotgun Ammunition
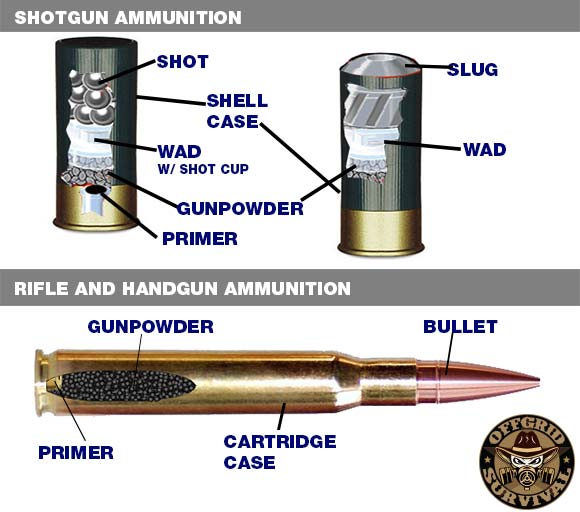
There are basically two types of ammunition, the cartridge and the shotshell. Rifle and handguns use a cartridge contain a projectile (bullet). Shotguns use a shotshell which contains either a number of small projectiles (known as shot) or a single projectile (known as a slug).
The components of both types of ammo are pretty similar; they both have the same basic components which include the case, the primer, gunpowder, and a projectile.
How does the ammo fire?
Ammunition is fired when a guns firing pin hits the ammo’s primer. This causes a spark from the primer to ignite the gunpowder. Gas is then converted from the burning powder which forces the projectile out of the case and down the barrel of the gun.
The illustration below shows the internal parts of both types of ammo.
What is the Best Self Defense Round?
This may shock a few people, but in my opinion, when it comes to handguns the best round is the round you have available. The fact is, even .22lr ammo is a perfectly acceptable self-defense caliber. In the hands of a skilled shooter, a .22lr round is just as effective as any other round in a self-defense situation.
When it comes to self-defense rounds, you often hear people talk about stopping power. While personally I would rather carry a 9mm over the .22, the fact is, any law enforcement officer who’s ever had to fire his weapon can tell you that even a 40 caliber round fired at center mass might not be enough to immediately stop an aggressor.
A good example of this can be seen an incident reported at lawofficer.com. Officer Peter Soulis, who was involved in a shootout during a routine traffic, pumped 22 shots into the aggressor, 17 of which hit center mass. Despite hitting the assailant so many time, the criminal was able to return multiple rounds of fire, and lived another 4 minutes after the last shot was fired.
In another great study on the stopping power of ammunition, it was found that the .22 caliber round was just as effective at stopping a criminal as any other round of ammunition. In fact, the .22 had one of the highest fatality ratings and one of the lowest number of rounds fired until incapacitation. In my opinion, this shows that shot placement is much more important than the round that’s being fired.
Is old ammunition safe to shoot?
It really depends on how the ammo was stored. Improperly stored ammo can be damaged by environmental conditions, especially humidity.
If I was buying something that had been in storage for a long amount of time, I would definitely be concerned with how that ammunition was stored. Improper storage can cause a whole host of problems. Primers can lose their sensitivity, charges can deteriorate, and cartridges can become brittle and even rupture when fired. You also have to watch out for corrosion problems that can actually change the size or characteristics of the ammunition.
How Should You Store your Ammo?
With the recent difficulties in finding ammunition supplies, more and more people are thinking about storing ammo for long periods of time.
Environmental conditions like extreme humidity can cause ammo to deteriorate pretty quickly. While the cardboard boxes that most ammo comes in should be sufficient for short-term storage, there are a couple of precautions that should be taken when storing ammo for long periods of time.
- Rotation Schedule: When it comes to ammo, I follow the same rules of food storage. I always fire the oldest ammo in my supply first; this insures that none of my ammo ever gets too old. Make sure you mark purchase dates on your ammo cans, so you use the oldest ammo first.
- Periodic Checks – If you’re not regularly firing your ammo, you need to rethink your preparedness strategy, because if you’re not practicing what’s the point of owning a gun? That being said, it’s a good idea to check your supplies at least once every three to six months for signs of corrosion.
- Vacuum Sealing your Ammo – Vacuum sealing your ammunition can help protect it from water, rust, and can even provide protection for those who bury it underground.
- Fight Humidity – Humidity is an ammo killer. If you can’t keep your ammo in a low humidity climate, you need to look into dehumidifying equipment. At the very least, you should place desiccant packets in all your ammo cans.
1.st timer…
Thank You! you really are helping people
GOD BLESS AMERICA!
I have a Model 10, Ruger, .22lr. My woman has a Glock, 9mm I bought her for Valentine’s Day. I am happy with both and so is she. We will show our guns to anyone who wants to see them. Anyone who tries to get froggy will get to hear them. Briefly.
Ooh, tough guy.
22 is good if you mean .223 trying killing a deer with 22 or a large motivated( drugs) individual stopping power has proven itself time and time again. Things are different in real life ill take 8 .45 or the extra weight of a real rifle. You wont have time to take abreath and aim for the smallest but most vulnerable part. you pick the biggest part and put as many bullets in it as the .23 seconds of a physical engagement can last. No hungry mass or rioting looters will be deterred by a 22 . Now a round that will go through 2 or three people before stopping is scary
I am not underscoring the supreme advantage to having a .22 rifle with a thousand rounds that weigh the same as 250 .223. I understand most small game have been taken since its inception with a .22. The 22 is in valuable just for survival out in the nowhere but in crazy town bigger always = badder. It’s called force multiplyer
I doubt many rioters have been heard to say “He’s only got a .22, let’s get him!” Maybe, “He’s only got a .22, YOU get him!”
If you are suggesting that a .45 is superior well i won’t argue. It is the Ford Chevy fight. However, if you don’t think a .22 LR or a 9mm will effectively work against a riot memeber, well stand out in a field and let me shoot you. If they wont effectively work against a riot member then they wont hurt you.
@Rob, Nice article for the basics, though I have a difference of thoughts on a few things. Rotation is right on and if you want to vacuum seal it, that’s fine but I’m not sure if it or even the inspection schedule is necessary. If the ammo is stored in “real” ammo cans with good seals, it should be good for years if stored out of the elements (not buried) and doesn’t reach VERY extreme HIGH temps. Also silica gel or other dehumidifiers should not be used inside the ammo cans. Ammo must have the “inherent” humidity of the powder kept intact to remain viable at acceptable and usable velocities and if desiccant is in the cans, when it removes all the humidity in the can it will then remove the humidity in the powder. In the military we store our munitions in the earthen “mounds” often seen on military installations. These are called igloos and they are anything but dry on the inside. Ammo is stored in the ammo cans, sans desiccants, but it will last for years. I have shot military ammo that was 40 years old or more with no problems other than corrosive primers (military safety officer, had to inspect the igloos, as well as use the ammo!). Now having said that, military ammo is sealed. Both the primer and the bullet itself are sealed with a lacquer. I do the same with my reloads for storage by using clear nail polish over the primers and the bullet to case interface. This one thing (and you can do it to commercial ammo as well)will do more to keep your ammo in good long-term shape than anything else, that and use good quality ammo cans. As far as direct burial, I don’t have any scientific, research based material on that but I would have to say that it would have to be buried with care and the fact that it is buried removes any reasonable inspection ability. A hidden bunker hole and storage without immersion in water (stored as mentioned above) and without ground contact would be the best way to store it out of sight rather than direct burial, though in this instance the vacuum sealing would prolly be useful and functional. Drafted in 72, retired in 10 JMHO. Be well.
Your A Good Man Trip… Thank You, For You!!
THE BEST SELF DEFENSE ROUND…I appreciate the intent, but this article is borderline dangerous. I have seen men die from a 22 caliber round, but it usually much later(infection, etc). The author requires a one-shot-stop to be a head/torso shot, yet those I’ve seen go down after a 45 ACP struck them in the hand, or a 357 magnum hit them in the elbow (effectively removing the limb). A bullet can AND DOES kill in minutes if a femoral artery is severed. As a PhD, this article wouldn’t make most journals because the author defines in a way that omits relevant data and presents bias into the study. I was hit in the leg by a 22 caliber round. It hurt & GOD intervened, but had the round been something like a 45 ACP or 357 Sig, the short term and long term consequences would probably have been much different. I’m sure the author is a good teacher and police officer, he is not a researcher. Do not trust this data.
I think the main point is that the rusty .22 you HAVE is better than the tricked-out AR15 you WANTED. I’ll take a single shot 12 guage over a ball bat any day. Don’t let the perfect be the enemy of the good.
I am pretty sure that bringing GOD into the equation when discussing research acumen completely destroys your credibility. Just saying.
I’m thinking more along the lines of having to be on the move. I don’t think bunking down anywhere is gonna be a long term option for most people should things really get bad. I think having to move around will probably be more relevant for most. In that case I’d rather carry a few thousand rounds of .22 as opposed to larger heavier ammo.
I can survive with a rifle, and fishing gear.
If I had to pack up and go those two things would be of most value to me.
I agree with the large clip idea. I’ll shoot until they stop moving or scatter. I keep a 9mm loaded with a 16 round clip and an extra clip loaded as well. If your shot can’t be quality, at least it can be quantity!
It’s a MAGAZINE(!) not a clip
what is your ip address just in case?
Here is some food for thought. Although the author is correct in what he says, the 22 requires a perfect shot. There is a reason that the Special Forces community is reviving the 45 ACP. It is the same reason that I carry a 45. When loaded with a hollow point it removes body parts. During the Philipine Insurection the military adopted the 45 because the 38 (the 38 and 9 MM are very similar) would not stop the enemy who were high and would wrap themselves with hemp rope. The Army had already adopted the 1911, however there were not enough in the inventory yet. The Army then went to the manufacturers and asked what they could get now that could shoot the 45 ACP. They got a revolver that with moon clips could shoot the 45.
Simply put the 45 will remove body parts. That will stop the attacker and you do not need that perfect shot. That is what this caliber is designed for. We use the 9 MM because of our allies.
I’d like to learn more about the types and sizes of certain ammunition what the grain sizes indicate and more detail if you have the time. Thank you.
Cheers!
They’ll get back to you next week.
Nice information. Thanks for sharing!
My boyfriend has a rifle round that he can’t identify I am hoping that you may be able to help him. The markings on the bottom part is CA B44
Thank you very much